CPU 스케줄링
CPU란?
프로그램의 기계어 명령을 실제로 수행하는 컴퓨터 내의 중앙처리장치.
일반적으로 시스템 내에 하나밖에 없으므로 여러 프로그램이 동시에 수행되는 시분할 환경에서의 CPU는 매우 효율적으로 관리되어야 하는 자원이다.
처리순서
- 프로그램이 시작되어 메모리에 올라간다.
- 프로그램 카운터라는 이름의 레지스터가 현재 CPU에서 수행할 코드의 메모리 주소값을 가지고 있다.
- CPU는 프로그램 카운터가 가르키는 주소의 기계어 명령을 수행한다.
CPU 스케줄러
CPU를 사용하는 패턴이 상이한 여러 프로그램이 동일한 시스템 내부에서 함께 실행되기 때문에 필요하다.
준비 상태에 있는 프로세스들 중에 어떠한 프로세스에게 CPU를 할당할지 결정하는 운영체제의 코드.
CPU스케줄링이 발생하는 상황
- 실행 상태에 있던 프로세스가 I/O 요청 등에 의해 봉쇄상태로 바뀌는 경우
- 실행 상태에 있던 프로세스가 타이머 인터럽트 발생에 의해 준비 상태로 바뀌는 경우
- I/O 요청으로 봉쇄 상태에 있던 프로세스의 I/O 작업이 완료되어 인터럽트가 발생하고 그 결과 이 프로세스의 상태가 준비 상태로 바뀌는 경우
- CPU에서 실행 상태에 있는 프로세스가 종료되는 경우
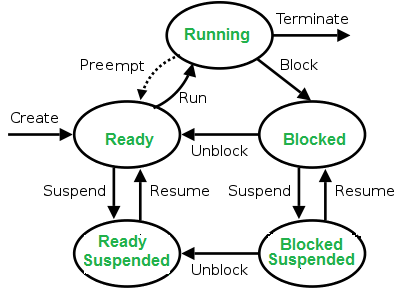
CPU 스케줄링 방식
비선점형 방식
CPU를 획득한 프로세스가 스스로 CPU를 반납하기 전까지는 CPU를 빼앗기지 않는 방법
일반적으로 선점형보다 스케줄러의 호출 빈도가 낮고 Context Switching 오버헤드가 작다.
(1), (4)가 대표적인 예.
선점형 방식
프로세스가 CPU를 계속 사용하기 원하더라도 강제로 빼앗을 수 있는 방법
"선점"이라는 말은 OS가 프로세스 자원을 선점하고 있다가 각 프로세스의 요청이 있을 때 특정 요건들을 기준으로 자원을 배분하는 방식 => 한 프로세스가 자원을 독점 할 수 없다.
(2), (3)이 대표적인 예
디스패처 dispatcher
CPU스케줄러가 어떤 프로세스에게 할당할지 결정하고 나면, 새롭게 선택된 프로세스가 CPU를 할당받고 작업을 수행할 수 있도록 환경설정하는 커널 모듈.
PCB에 저장, 복원 등등.. 소요 시간은 Context Switching 오버헤드에 해당.
스케줄링 알고리즘
FCFS
FCFS(First-Come First-Served)는 프로세스가 준비 큐에 도착한 시간 순서대로 CPU 할당
프로세스가 자발적으로 CPU를 반납할 때까지 CPU를 선점하지 않는다. => 비선점형 방식
단점 : Convoy(콘보이) 현상
CPU버스트가 짧은 프로세스가 CPU버스트가 긴 프로세스보다 나중에 도착해 오랜 시간을 기다려야 하는 상황.
(CPU를 짧게 사용해야 하는 프로세스가 길게 사용해야하는 프로세스보다 나중에 도착해서 무한 대기)
SJF
SJF(Shortest-Job First)는 CPU 버스트가 가장 짧은 프로세스에게 먼저 CPU를 할당하는 방식.
프로세스들이 준비큐에서 대기하는 전체적인 시간이 줄어든다.
비선점형
일단 CPU를 획득하면 자진 반납할때까지 선점 당하지 않는 방식.
선점형
준비 큐에서 CPU버스트가 가장 짧은 프로세스에게 CPU를 할당했다 하더라도 더 짧은 프로세스가 도착할 경우 CPU를 빼앗아 부여한다. ==> SRTF(Shortest Remaining Time First)
일반적 시분할 환경에서는 평균 대기 시간을 가장 많이 줄일 수 있는 방식.
단점 : CPU 버스트 시간을 미리 알수 없다.
그렇기 때문에 예측치가 가장 짧은 프로세스에게 할당한다.
기아 현상(Starvation)
계속 CPU버스트가 짧은 프로세스에게만 할당할 경우 CPU 버스트가 긴 프로세스는 준비 큐에서
무한 대기
우선순위 스케줄링
준비큐에서 기다리는 프로세스들 중에 우선순위가 가장 높은 프로세스에게 CPU할당
숫자가 낮을수록 우선순위가 높다.
비선점형
비록 우선순위가 더 높은 프로세스가 도착하더라도 CPU를 자진 반납하기 전까지 선점 불가.
선점형
현재 CPU에서 수행중인 프로세스보다 우선순위가 높은 프로세스가 도착할 경우 CPU를 새롭게 도착한 프로세스에 할당.
단점: 기아 현상(Starvation) 우선순위가 낮은 프로세스는 무한대기.
=> 에이징 기법
에이징 기법이란 기다리는 시간이 길어지면 우선순위를 조금씩 높여 언젠가 가장 높은 우선순이가 되어 CPU를 할당받을 수 있게 해주는 방법.
HRN 스케줄링
HRN(Highest Response-ratio next)는 SJF의 단점을 보안하기 위해 등장.
우선순위 계산식을 이용하여 자원 할당. 숫자가 높을수록 우선순위가 높다. ==> 비선점형
우선순위 = (대기시간+실행시간)/실행시간
라운드 로빈 스케줄링
시분할 시스템의 성질을 가장 잘 활용한 새로운 의미의 스케줄링 방식.
CPU 사용 시간이 특정 시간으로 제한되며, 이 시간이 경과되면 CPU를 회수해 다음 프로세스에게 할당하고, 이 프로세스는 준비 큐의 맨 뒤로 가서 차례를 기다린다. ==> 선점형
라운드 로빈 스케줄링은 SJF방식보다 평균대기시간은 길지만 응답시간은 더 짧다.
할당시간 : 각 프로세스가 CPU를 연속적으로 사용할 수 있는 최대 시간.
할당시간이 너무 길면 FCFS와 같은 결과를 초래할 수 있으며, 너무 작으면 빈번하게 교체로 인한 context switching 오버헤드가 커지게 된다.
CPU를 회수하는 방법으로는 타이머 인터럽트 사용. 만약, CPU 버스트 시간이 할당시간보다 짧으면 자신의 버스트 시간만큼 스스로 사용후 반납.
'Computer Science > Operating System' 카테고리의 다른 글
| 가상메모리(virtual memory)와 요구페이징(demand paging) (1) | 2019.04.19 |
|---|---|
| 프로세스 동기화 (Process Synchronization) (1) | 2019.04.17 |
| 스케줄러 Scheduler (0) | 2019.02.23 |
| 프로세스, 쓰레드, 멀티프로세싱, 멀티쓰레드 (0) | 2019.02.15 |